해당 내용은 20년 2학기 COSE354 "정보보호" 수업 중간 텀 프로젝트로 제출한 최지현의 보고서입니다.
추가: 2020년도 암호경진대회 1번 문제라고 합니다. https://ghqls0210.tistory.com/6
Given project:
"HRDKHUBHAAMAEQMTMZSHGBAKFUBHAASYRXUNKYUAATQCTLUTOGEWVAJGVEIIYTKIOTQRXXQVSQLISVVOCNGCUXPKPIUBOHTVKCFKWNJSEZYSSUTUOESIXKAPVFXNZHAOQTLCGYJVAEHLNNKEESQMKSHKKDFCNZSRHRDKHSDKFXVPTGMKRUPZBIKEVNYEKXMFXKFYMWYUDZDENEWNKDAOUXGPCXZDLCSNFGCMCSNUAOJDBLQTAHEWYZCHQJYKSNUWOKQKONZGOKDXGUXKEMWQMCFGUEAVKHDIIATCHVTGYMGKJMLNPCNAYKMIRWEETIYQKELEGLQOVKISFNUDAJQIQYBXQTMZSHGBAKFZRCNWRSODAFKKXWGAZGDBIUDDHCUDFRFOVSZXADSHYSGLTQBMNEMKDCFSOZSRDYLIHIAXCMGMFEIDNZKOVJEOIEFNWWQEDRLZYZIZXADSHYSGLJYFWDUAKSIOGOZOXWYPBUFEPNBIRJUJNDZJJYMURKNCIKPWLRMRIAGVSXTYNIWPROHLDHQOMBEKZURQCLQOVKISFNUAFQBHGPCLHZTPJVPXIZKLQSNVKIJAEITTNVSVWNFYVATDEMKDCTGIHKZTVGZYXTYQEDBACFMNCAHRDKHSDKFXZXXGMJOSLPSZBMOILMMWRALAFFMNXXDYFBIYQVVOHSWKGBIRJGTBYQLKIJAEQBTAXGFGAVUIJADHQKLFWRJXYFVIGGQZNBHSUIYOZALSKIABLWQNXNXKOAJAIKHXODXWORVDOGBMHOPLQJZALQJZALIKTKLENZHQAVYUEUFEVLUXHGOWNMGWXUIAHGQOMNCKFQLIPBNKVWDLNGMJCOBFKIGBYWPAHMMPQLUTOGECXITZVVAJEOIDCNWMFNLOBGQXCYFWQFWVXWRKWYGBFHJVLBAWBOUQEKHZHSZZIZARYITDCLQFPGBTJMQVSQLIHPEJONCYMZWTVJVZOBOMOHPSXMPUKVAGXIPOQUQUQBCKXZJSZAHEWYHAEMKOJCCCFBEUKVNCAWANSNXISVVOWHQGQFBGWKQEGBIFRGIZUJQWIMFANTGBHWGVAGXIPOQUQTTRMWDHDGRFENKYPZVCLNQAUBTZSRYGVGOWSVROENABMZTOHZRQFUEVPLLIODEYRYLUTOGPYAFHJFIVOSFMPBSHLEKWYWJYTFYETAZQCRFTFHOMACOQVTWKLKYMGIMQDSYNWMFNIEITWMBVVWANBQFVUSKZOTLCCWABAGHWZBZHRDKHDTUOMUUUGQICHNUUQFJYUCQUO"
This ciphertext is given. It uses Hill encryption method. You know nothing about the key, even the key size. Find the plaintext.
Introduction
In order to decrypt a Hill cipher, usually one plaintext and ciphertext pair is given, and through those pairs, we calculate the key matrix, by using inverse matrix multiplication. However, under the circumstances given in this particular project, we know nothing about a plaintext and nothing about the key, even the length of the key. In this situation, we can use alphabet frequency statistics to break the cipher.
Body
Brute force search for key and time complexity
Usually if we know nothing about the key, in order to attack the cipher, the attacker would use Brute-force search to find the key. Then, after the Brute-force search, the attacker would compare the decrypted ciphertext’s observed alphabet frequency with the normal alphabet frequency. If the frequency is similar, the likelihood that the key is correct goes up. However, when using Brute-force search for every possible key, the time complexity is too high. If the key is d*d long, the time complexity becomes about O(26d*d) (every element of the matrix has a possibility of 26 different numbers).
Therefore, in my solution, some measures have been taken to reduce the time complexity. In order to describe my measures, explanation should be given about mathematical characteristics of matrix multiplication in Hill cipher and how that characteristic can be used to solve the Hill cipher without any information about the key.
Determining key size
First, in order to approach the key, determining the key size is most important. Decryption key (inverse of the encryption key) is denoted K-1. The plaintext P can be found if we multiply ciphertext C with the matrix K-1 . If K-1is a size of d*d, C can be of any length but it has to be a multiple of number d. In this case, the ciphertext’s length is 1285, so the key size can be either 5 or 257, both being prime numbers. For this project, I tried with 5*5 key size first and it worked.
Using “columns”
Multiplication of matrixes to decode/encode messages in Hill cipher requires multiplying a 1*d matrix (whether it is plaintext or ciphertext) with the key(or to decrypt a message, the inverse of the key). Therefore, we should observe the inverse key by column. In detail, the first element of the plaintext is derived by calculation(multiplication and addition) of the elements of ciphertext with the inverse key’s first column...and so on. So my first observation was that to find the key, we should approach with “columns”. If we approach with columns, we can reduce the time complexity because instead of trying d*d entire matrix, only a column d*1 is observed. (O(26d ) instead of O(26d*d )).
In this project, to find K-1; not 265*5; brute-force search was needed, but 265 brute-force search was needed. Just brute-force to find 5*1 elements was needed.
However, when solving the problem with an approach to columns, it may be difficult to find the correct matrix, since a matrix consists of many columns with a specific order. Therefore, after figuring out what the columns are, the process for finding the specific order of those particular columns is needed. In other words, to find the matrix key with an approach of “columns”, we cannot know the exact permutation. The exact permutation can be found easily whether by using bigram frequency, or just printing out the decrypted plaintext by size of columns and find a plausible looking order.
To use columns, splitting the plaintext or ciphertext is needed. The messages should be split in the length of d, making n(length of ciphertext)/d d-sized groups. For instance, for the project, n is 1285, and d is 5. So, the ciphertext can be split, making 257 blocks (c0 ~ c256, each 5 elements long).
Index of maximum likelihood
As mentioned before, in ordinary approach that requires high time complexity, brute-force, which is searching all 26 possibilities for d*d key elements, is done first, then, use the monogram table to find a plaintext with high likelihood. This takes up too much time, so we must find another way, which is using the index of maximum likelihood. If we use the concept of index of maximum likelihood, (or IML), we can update this value depending on whether the given string is meaningful monogram-wise.
Checking this IML can be used when using the candidate of K-1 , decrypt C and get P, and to verify this P is monogram-wise meaningful. As mentioned before, we are approaching in terms of columns, so if there is a block of C, for instance using the column of K-1, decrypt c0; and get p0; ....and so on. For all these strings, we can update the IML. The higher IML, the better, and if this IML is over some extent, we say that it is monogram-wise meaningful.
To find the some “extent” mentioned on the previous explanation, this “extent” can be the highest IML for the decrypted string, and in order to find that highest IML, we can make an arbitrary K-1 and calculate K-1’s IML(in terms of columns). Using the column matrix produced by the brute-force search, we can compare whether that column matrix has a higher IML than that of K-1. If that column has a higher IML, than it can replace the column of K-1
So, how can we calculate IML? In order to find the IML of a string P, we should know two types of frequencies, which is observed frequency and correct frequency(monogram frequency). Observed frequency is the frequency in the string itself. The correct frequency is the frequency that is denoted in the monogram table. For an ith letter of the alphabet, if we multiply the observed frequency of i with log2(correct frequency of i), and add all these values, then -IML(P) is calculated.
Eliminating repeated calculations and Precomputation
Using precomputations and eliminating repeated calculations, we can also reduce time complexity. The time complexity on searching the columns of the key by brute-force was O(26d*d), and if these eliminating calculations or precomputation was not at place, the whole algorithm of finding the key should have been O(d2 * 26d). But through these measures, the algorithm is reduced to O(d* 26d) using divide and conquer.
The main point of precomputation has to do with characteristics with matrixes. Mentioned previously, we do, brute-force search to find columns, lexicographically, which means there is an order when we do this computing. Let’s say there is a column vector x, and x’ is the precedent vector of x, which is possible, because it is done lexicographically. x is a part of K-1, so acts as an inverse of an key. Since multiplying inverse of a key with ciphertext means plaintext, is pi = x' * ci definitely possible. ci*x is pi, so we can use pi to find a relationship between ci *x and ci *x’, and this can be precomputed. Let’s say (transposition matrix) xT is [0,.....0, xt +1, xt+1 ....... ]. Since the precedent matrix x'T is lexicographically precedent, it is [25,.....25,xt, xt+1 .......xd ] (mod 26). By lexicographically precedent, we mean from the right-most element, when comparing two row matrixes, if one matrix’s rightmost value is smaller than the other matrix’s rightmost value, it precedents it, if the value is the same, then we compare the next right-most element...and so on. If there are t zeroes in front of x, then there are t 25s in front of x’ too. if we do x-x’ (mod 26) , then a column matrix consisting of only 0 and 1 is found. There are t+1 1s at the top, and other elements are all 0s. When multiplying ci with (x-x’), we can find out that the values are the sum of the starting t+1 elements of ci. We precompute these values and save them in d(i,t), and use them during the brute-force search for x, calculating the estimated plaintext.
Finding the plaintext
After finding the suitable K-1 , we can decrypt the cyphertext by multiplication of matrixes. However, the problem was that, as mentioned before, K-1itself cannot be used directly to obtain the right plaintext, rather, we should do some permutation or order changing of columns. Therefore, in order to find the right permutation, the easiest way was to find what order looked more plausible. I needed to change the entire order by rearranging columns, so I first printed out the plaintext without correct permutation, with 5 letters at one row. Then, I could find the most suitable plaintext.
Conclusion
The whole process of breaking the Hill cipher in this project had to do with mathematical concepts, and especially in this particular project, it had a lot to do with linear algebra. Through using these kinds of mathematical ideas, we can decrypt the ciphertext without any information about the key and given ciphertext’s plaintext pair.
The main strategies for solving the problem was using the concept of “columns” in matrixes, and trying to minimize the time complexity, which in my solution, was O(d*26d ).
References
1. S Khazaei, S Ahmadi. Ciphertext-only attack on d×d Hill in O(d13d), IACR Cryptology ePrint Archive, 2015.
Appendix
Source code (images) with comments
[Image 1 (line 1~20)]
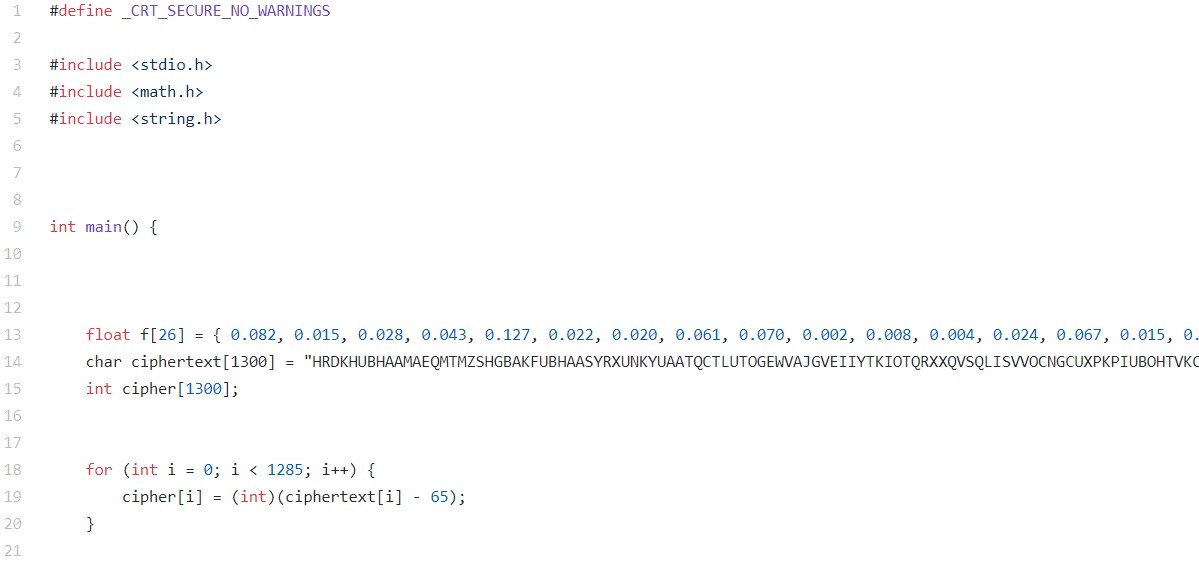
In float array “f”, the frequency of each alphabet using the monogram frequency table is saved. For instance, f[0] which is 0.082, is the frequency of ‘A’ in English language, f[1] which is 0.015 is the frequency of ‘B’. In char array “ciphertext”, the ciphertext is saved in string format. The for Loop in the 18th line uses the ascii code to convert the alphabet form of ciphertext into integer form. The integer form is saved in the int array “cipher”.
[Image 2 (line 24~43)]

“d” is the key size for d*d size key matrix. For an “n”-length ciphertext, this ciphertext can be broken into “m” ciphertexts with the length of “d”. In this case, 1285 length ciphertext can be broken into 257 ciphertexts with length of 5. Int array C is the divided ciphertext. Because the array “cipher” includes the elements in 1-dimensional array, it should be converted to 2-dimensional arrays. 2-dimensional array “dit” is precomputed in the for Loop, in a way as mentioned before.
[Image 3 (line 54~82)]

First, int array “inverseK” is the inverse of the key, which we have to wind up finding. The float array “I” is an array that saves the value of IML of each column of matrix “inverseK”. Int array “p” is an array that represents a decrypted letter that is generated through the columns of “inverseK”. variable “iml” is index of maximum likelihood. It is first set to log2 f[0], because p[1]~p[5] are zero.
The loop of x4~x0 represents a brute force search for one column. The column is generated in array form, named “xmembers”. For these “xmembers”, the number of continuing zeroes from the top of the column is counted by variable “t”. If the column is all zeros, it is not a factor we consider so only when “t” is not 5, the for Loop is executed. In the for Loop, the value of “iml” is changed, and “p[i]” also is changed. The value of “p[i]” depends on “dit[i][t]”. All the number of “dit” is already precomputed in the previous lines, so in this part, we just add this dit[i][t] to the previous p[i] and make a new p[i].
[Image 4 (line 84~119)]
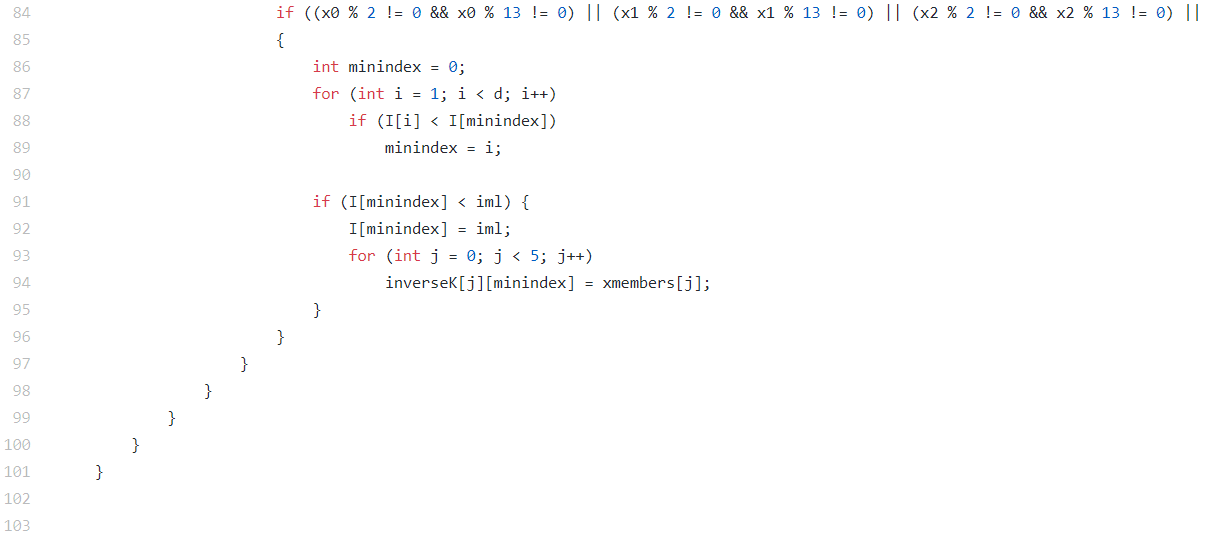
Down to line 101, the if statement is included in the for Loop deciding the “xmembers” with brute force search in the previous image(Image 3). The reason why x0~x4 should not be all zeros when doing modular 2 or modular 13 is that trying 26d possibilities is approximately similar to trying 2d-1, 13d-1possibilities independently. Inside the if statement, what the for Loops are trying to do is trying to maximize the values of iml, so it is keeping track of the minimum index in the variable “minindex”. After all these procedures, the most meaningful K-1is found.
The inverse of key K is found, the result is printed.
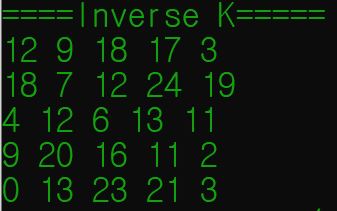
[Image 5 (line 120~138)]

int array “P” is the plaintext decrypted by the inverse of the key. The plaintext can be acheived through multiplication and addition process of the array “C” with the array “inverseK”.
The plaintext is acheived, however, it is not in correct permutation form. The columns can be switched, therefore, print the array “P” so that only 5 characters per line is printed.
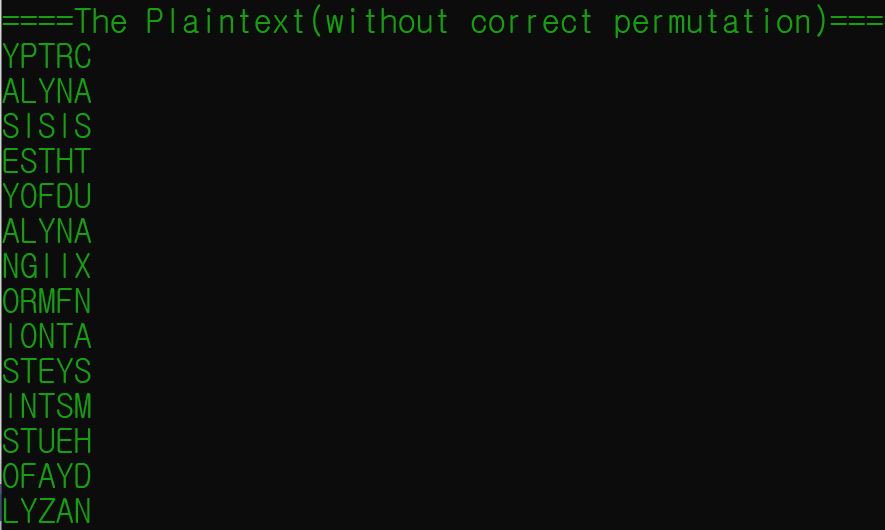
Depending on the compiler, it shows different results, some debugger showing a slightly different result with different permutation.
[Image 6 (line 140~149)]

After observing the plaintext without correct permutation, we can have 5! permutations, but just by looking at the first line of the plaintext, we can guess what the correct permutation is because there is one that is plausible. The plausible order is 5th column comes first for every line, then 4th, 1st, 2nd, 3rd. So, switch the order of columns so that a plausible looking plaintext is printed.
For the same compiler used in the above (shown on image 5), the correct permutation order is column 5th ,4th, 1st, 2nd, 3rd
Entire Source code
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <math.h>
#include <string.h>
int main() {
float f[26] = { 0.082, 0.015, 0.028, 0.043, 0.127, 0.022, 0.020, 0.061, 0.070, 0.002, 0.008, 0.004, 0.024, 0.067, 0.015, 0.019, 0.001, 0.060, 0.063, 0.091, 0.028, 0.010, 0.024, 0.002, 0.020, 0.001 };
char ciphertext[1300] = "HRDKHUBHAAMAEQMTMZSHGBAKFUBHAASYRXUNKYUAATQCTLUTOGEWVAJGVEIIYTKIOTQRXXQVSQLISVVOCNGCUXPKPIUBOHTVKCFKWNJSEZYSSUTUOESIXKAPVFXNZHAOQTLCGYJVAEHLNNKEESQMKSHKKDFCNZSRHRDKHSDKFXVPTGMKRUPZBIKEVNYEKXMFXKFYMWYUDZDENEWNKDAOUXGPCXZDLCSNFGCMCSNUAOJDBLQTAHEWYZCHQJYKSNUWOKQKONZGOKDXGUXKEMWQMCFGUEAVKHDIIATCHVTGYMGKJMLNPCNAYKMIRWEETIYQKELEGLQOVKISFNUDAJQIQYBXQTMZSHGBAKFZRCNWRSODAFKKXWGAZGDBIUDDHCUDFRFOVSZXADSHYSGLTQBMNEMKDCFSOZSRDYLIHIAXCMGMFEIDNZKOVJEOIEFNWWQEDRLZYZIZXADSHYSGLJYFWDUAKSIOGOZOXWYPBUFEPNBIRJUJNDZJJYMURKNCIKPWLRMRIAGVSXTYNIWPROHLDHQOMBEKZURQCLQOVKISFNUAFQBHGPCLHZTPJVPXIZKLQSNVKIJAEITTNVSVWNFYVATDEMKDCTGIHKZTVGZYXTYQEDBACFMNCAHRDKHSDKFXZXXGMJOSLPSZBMOILMMWRALAFFMNXXDYFBIYQVVOHSWKGBIRJGTBYQLKIJAEQBTAXGFGAVUIJADHQKLFWRJXYFVIGGQZNBHSUIYOZALSKIABLWQNXNXKOAJAIKHXODXWORVDOGBMHOPLQJZALQJZALIKTKLENZHQAVYUEUFEVLUXHGOWNMGWXUIAHGQOMNCKFQLIPBNKVWDLNGMJCOBFKIGBYWPAHMMPQLUTOGECXITZVVAJEOIDCNWMFNLOBGQXCYFWQFWVXWRKWYGBFHJVLBAWBOUQEKHZHSZZIZARYITDCLQFPGBTJMQVSQLIHPEJONCYMZWTVJVZOBOMOHPSXMPUKVAGXIPOQUQUQBCKXZJSZAHEWYHAEMKOJCCCFBEUKVNCAWANSNXISVVOWHQGQFBGWKQEGBIFRGIZUJQWIMFANTGBHWGVAGXIPOQUQTTRMWDHDGRFENKYPZVCLNQAUBTZSRYGVGOWSVROENABMZTOHZRQFUEVPLLIODEYRYLUTOGPYAFHJFIVOSFMPBSHLEKWYWJYTFYETAZQCRFTFHOMACOQVTWKLKYMGIMQDSYNWMFNIEITWMBVVWANBQFVUSKZOTLCCWABAGHWZBZHRDKHDTUOMUUUGQICHNUUQFJYUCQUO";
int cipher[1300];
for (int i = 0; i < 1285; i++) {
cipher[i] = (int)(ciphertext[i] - 65);
}
int m = 257;
int d = 5;
int C[260][5];
for (int i = 0; i < m; i++) {
for (int j = 0; j < d; j++) {
C[i][j] = cipher[i * 5 + j];
}
}
int dit[260][5];
for (int i = 0; i < m; i++) {
int sum = 0;
for (int j = 0; j < d; j++) {
sum += C[i][j];
sum %= 26;
dit[i][j] = sum;
}
}
int inverseK[5][5] = { 1, };
float I[5] = { -9999,-9999,-9999,-9999,-9999 };
int p[260] = { 0, };
float iml = -log2f(f[0]);
printf("Loading....\n");
for (int x4 = 0; x4 < 26; x4++) {
printf("Loading...%f\n", (float)x4/26);
; for (int x3 = 0; x3 < 26; x3++) {
for (int x2 = 0; x2 < 26; x2++) {
for (int x1 = 0; x1 < 26; x1++) {
for (int x0 = 0; x0 < 26; x0++) {
int xmembers[5] = { x0, x1, x2, x3, x4 };
int t = 0;
for (t = 0; t < 5; t++) {
if (xmembers[t] != 0)
break;
}
if (t != 5) {
for (int i = 0; i < m; i++) {
iml -= log2f(f[p[i]]) / m;
p[i] = (p[i] + dit[i][t]) % 26;
iml += log2f(f[p[i]]) / m;
}
}
if ((x0 % 2 != 0 && x0 % 13 != 0) || (x1 % 2 != 0 && x1 % 13 != 0) || (x2 % 2 != 0 && x2 % 13 != 0) || (x3 % 2 != 0 && x3 % 13 != 0) || (x4 % 2 != 0 && x4 % 13 != 0))
{
int minindex = 0;
for (int i = 1; i < d; i++)
if (I[i] < I[minindex])
minindex = i;
if (I[minindex] < iml) {
I[minindex] = iml;
for (int j = 0; j < 5; j++)
inverseK[j][minindex] = xmembers[j];
}
}
}
}
}
}
}
printf("====Inverse K=====\n");
for (int i = 0; i < d; i++) {
for (int j = 0; j < d; j++) {
printf("%d ", inverseK[i][j]);
}
printf("\n");
}
int P[260][10] = { 0, };
for (int p = 0; p < m; p++) {
for (int q = 0; q < d; q++) {
int ksum = 0;
for (int r = 0; r < d; r++) {
ksum = ksum + (C[p][r] * inverseK[r][q]);
}
P[p][q] = ksum % 26;
}
}
printf("====The Plaintext(without correct permutation)=====\n");
for (int i = 0; i < m; i++) {
for (int j = 0; j < d; j++)
printf("%c", (char)(P[i][j] + 65));
printf("\n");
}
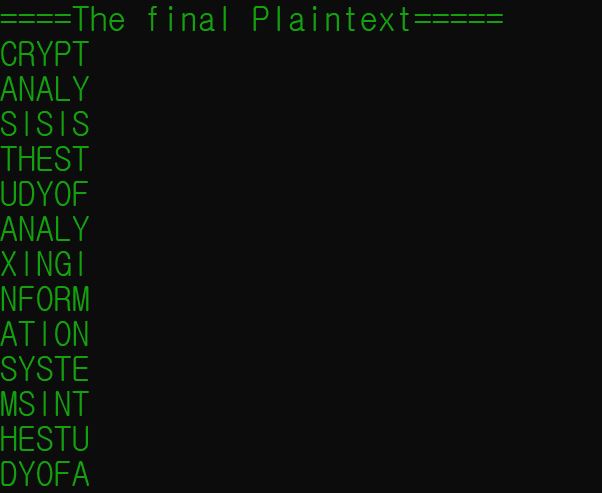
printf("====The final Plaintext=====\n");
for (int i = 0; i < m; i++) {
printf("%c", (char)(P[i][4] + 65));
printf("%c", (char)(P[i][3] + 65));
printf("%c", (char)(P[i][0] + 65));
printf("%c", (char)(P[i][1] + 65));
printf("%c", (char)(P[i][2] + 65));
printf("\n");
}
}Decrypted Ciphertext
CRYPTANALYSIS IS THE STUDY OF ANALYXING INFORMATION SYSTEMS IN THE STUDY OF ANALYZING INFORMATION SYSTEMS
IN ORDER TO STUDY THE HIDDEN ASPECTS OF THE SYSTEMS CRYPTANALYSIS IS USED TO BREACH CRYPTOGRAPHIC
SECURITY SYSTEMS AND GAIN ACCESS TO THE CONTENTS OF ENCRYPTED MESSAGES EVEN IF THE CRYPTOGRAPHIC
KEY IS UNKNOWN IN ADDITION TO MATHEMATICAL ANALYSIS OF CRYPTOGRAPHIC ALGORITHMS CRYPTANALYSIS
INCLUDES THE STUDY OF SIDE CHANNEL ATTACKS THAT DO NOT TARGET WEAKNESSES IN THE CRYPTOGRAPHIC
ALGORITHMS THEMSELVES BUT INSTEAD EXPLOIT WEAKNESSES IN THEIR WEAK IMPLEMENTATION EVEN THOUGH THE
GOAL HAS BEEN THE SAME THE METHODS AND TECHNIQUES OF CRYPTANALYSIS HAVE CHANGED DRASTICALLY THROUGH
THE HISTORY OF CRYPTOGRAPHY ADAPTING TO INCREASING CRYPTOGRAPHIC COMPLEXITY RANGING FROM THE PEN AND
PAPER METHODS OF THE PAST THROUGH MACHINES LIKE THE BRITISH BOMBES AND BOLOSSUS COMPUTERS AT
BLETCHLEY PARK IN WORLD WAR TWO TO THE MATHEMATICALLY ADVANCED COMPUTERIZED SCHEMES OF THE
PRESENT METHODS FOR BREAKING MODERN CRYPTOSYSTEMS OFTEN INVOLVE SOLVING CAREFULLY CONSTRUCTED
PROBLEMS IN PURE MATHEMATICS THE BEST KNOWN BEING INTEGER FACTORIZATION GIVEN SOME ENCRYPTED DATA
THE GOAL OF THE CRYPTANALYST IS TO GAIN AS MUCH INFORMATION AS POSSIBLE ABOUT THE ORIGINAL UNENCRYPTED
DATAT IS USEFUL TO CONSIDER TWO ASPECTS OF ACHIEVING THIS THE FIRST IS BREAKING THE SYSTEM THAT IS DISCOVERING
HOW THE ENCIPHERMENT PROCESS WORKS THE SECOND IS SOLVING THE KEY THAT IS UNIQUE FOR A PARTICULAR
ENCRYPTED MESSAGE OR GROUP OF MESSAGE
'전공수업 > 정보보호' 카테고리의 다른 글
| [전공수업][정보보호] Discrete Logarithms (0) | 2020.11.20 |
|---|---|
| [전공수업][정보보호] Miller-Rabin Test (0) | 2020.11.20 |


댓글